RCM

The Rice Convection Model (RCM) is an established physical model of the inner and middle magnetosphere that includes the coupling to the ionosphere. It uses a many-fluid formalism to describe adiabatically drifting isotropic particle distributions in a self-consistently computed electric field and specified magnetic field. The RCM represents the particles in terms of multiple fluids. Its equations and numerical methods have been specifically designed for accurate treatment of the inner magnetosphere, including the flow of electric currents along magnetic field lines to and from the conducting ionosphere. The standalone RCM computes these currents and the associated electric fields self-consistently. When coupled to other models, such as GAMERA, the electric fields are provided by these models. It assumes perfectly conducting field lines and employs a pre-computed time-dependent magnetic field with associated induction electric fields. The RCM algorithms have been described in different publications (e.g., Harel et al., 1981; Sazykin 2000; Toffoletto et al., 2003). The outer boundary of the model can be placed either as far away from the Earth as possible while still remaining in the region of closed magnetic field lines and sub-Alfvenic flow speed, or it can be positioned at the geosynchronous (L=6.6) orbit to take advantage of the particle flux data available. The inner boundary is set at L=1.01. The plasma population is typically represented by 75-150 proton and 25-30 electron isotropic "fluids" with associated energy invariants. The RCM grid is polar that is fixed in the ionosphere with variable grid spacing in latitude (typically finer near the auroral zone) and constant in local time. Typical grid sizes are ~200 in latitude and ~100 in local time.

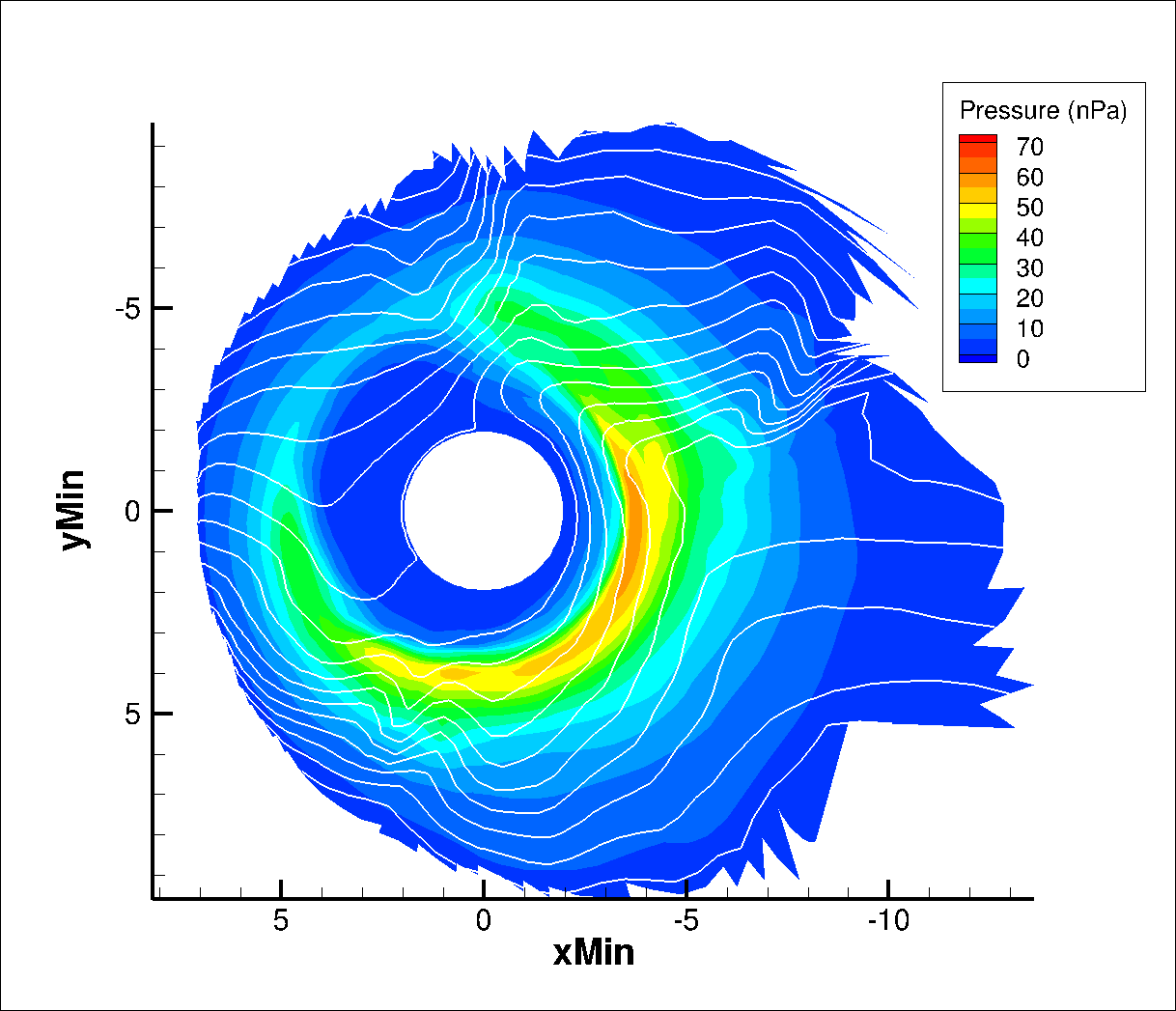
The figure above shows the RCM computed pressure in the equatorial plane (Sun to the left) when two-way coupled to GAMERA. The lines are equipotential contours, spaced at 10 kV intervals.