GAMERA

History

LFM code was rewritten by J. Lyon, J. Fedder and C. Mobarry at NRL in the 1980's. Its heritage is traced back to pioneering work on Flux Corrected Transport (FCT) schemes in the same group (J. Boris, D. Book, S. Zalesak, K. Hain). Initial simulations started with very high order spatial interpolation schemes (e.g., 20th order), which was later reduced to 8th order standard today. Over the years, the LFM code or its derivatives have been applied to the terrestrial magnetosphere, planetary magnetospheres (Saturn, Neptune, Uranus, Venus), to inner and outer heliosphere, and regional magnetotail simulations. In 2000's the code was MPI-parallelized which allowed very high resolution simulations reproducing magnetopause boundary instabilities (Kelvin-Helmholtz) and flux-tranfer events (FTEs), ionospheric field-aligned currents with remarkable resemblence to observations, and dipolarization fronts in the magnetotail. Also in 2000's, as part of the Center for Integrated Space Weather Modeling (CISM), a geospace model coupling framework was developed, which allowed implementation of coupling with the Rice Convection Model (RCM) of the inner magnetosphere and the NCAR TIEGCM model of the ionosphere-thermosphere. Finally, in the late 2000's LFM was extended to include the capability to simulate multiple ion fluids. This extension has become known as Multi-Fluid LFM (MFLFM).

2-D LFM simulation of the terrestrial magnetosphere using 50x40 grid cells. Adapted from Lyon et al. (1981), Computer Simulation of a Geomagnetic Substorm. Phys. Rev. Lett., 46(15), 1038–1041.

Magnetosphere simulation of a southward rotation of the interplanetary magnetic field using the modern high—resolution version of the LFM code (212x192x256 grid cells). The view is from the post-noon sector, above the equatorial plane. Current density in the meridional plane indicates sharply resolved bow shock and the magnetopause. The equatorial plane shows the residual magnetic field indicating Kelvin-Helmholtz instability on the magnetopause boundary and dipolarization fronts in the magnetotail. The dayside magnetic field lines also indicate occasional flux ropes interpreted as flux transfer events (FTEs).

Inner heliosphere simulation of a coronal mass ejection using the LFM code coupled with a corona simulation by the MHD algorithm outside a sphere (MAS) code. The grid is heliocentric; the inner boundary of the LFM code (at 30 solar radii) and the equatorial plane show the solar wind speed. The magnetic field lines are color coded with the geoeffective Bz component of the interplanetary magnetic field. Adapted from Merkin et al., (2016), Coupling of Coronal and Heliospheric Magnetohydrodynamic Models: Solution Comparisons and Verification. Astroph. J., 831(1), 23.

LFM simulation of the Jovian magnetosphere indicates the dawn-dusk asymmetry in Kelvin-Helmholtz waves, a Rayleigh-Taylor-like instability in the inner magnetosphere, magnetic plasmoids shed by the night side reconnection line, as well as the auroral signatures on the inset in the lower left corner. See also Zhang et al., (2018), Asymmetric Kelvin-Helmholtz instability at Jupiter's magnetopause boundary: Implications for corotation-dominated systems. Geophys. Res. Lett., 45, 56–63.

Comparison of a real event LFM simulation compared with ionospheric Birkeland currents inferred from the Active Magnetosphere and Polar Electrodynamics Response Experiment (AMPERE) demonstrate at times remarkable agreement provided a sufficiently high-resolution simulation grid is used. Adapted from Merkin et al., (2013), Global evolution of Birkeland currents on 10 min timescales: MHD simulations and observations. J. Geophys. Res., 118(8), 4977–4997.

Previous Next

Applications

GAMERA was written in a very flexible way and allows easy adaptation to different geometries and initial/boundary conditions via user files. The primary current applications are the terrestrial magnetosphere, the inner heliosphere/solar wind, magnetospheres of outer planets, current sheets and reconnection, and MHD instabilities (e.g, Kelvin-Helmholtz and Rayleigh-Taylor.)

Algorithms

• Curvilinear grids
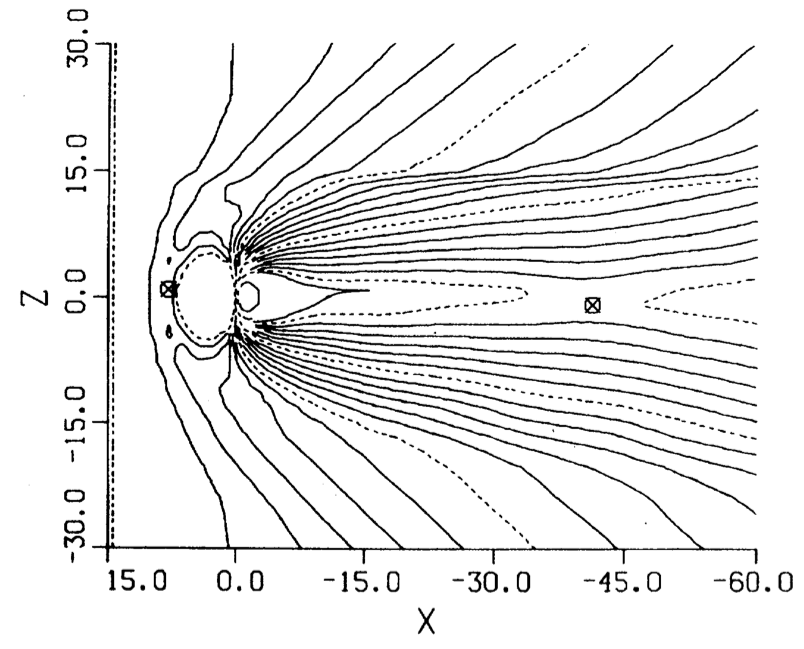
  • A key distinguishing feature of the LFM/GAMERA MHD algorithm is its finite-volume formulation allowing arbitrary (including non-orthogonal) hexahedral grids.
  • This allows adapting the grid to the geometry of the problem (e.g., packing more grid cells around the magnetopause in magnetospheric calculations) and overall high resolving power with a relatively small total number of grid cells.
  • GAMERA improves on the previous LFM algorithm by employing a higher order metrics calculations (12th order Gaussian quadrature.)
• Partial interface method
• High (7th or 8th) order spatial interpolation of conserved variables.
• Aggressive Partial Donor Cell (PDM) Limiter and Left/Right state splitting on primitive variables. Clipping and non-clipping options.
• Flux calculation uses the gas-kinetic method. However, implementation is flexible and other flux functions can be used.
• Constrained transport (magnetic flux are defined at cell faces, while electric field is defined at cell edges) keeps magnetic field divergenceless to round-off error.
• Pole axis treatment (Ring Average) for spherical and cylindrical geometries.
• Background magnetic field subtraction is necessary in magnetospheric simulations to remove the dominant planetary dipole from field calculations.
• Conservative and semi-conservative energy equation treatment (total and plasma energy formulations.)
• Boris correction is critical in magnetospheric simulations where Alfvén speed becomes prohibitevly large near the planet.
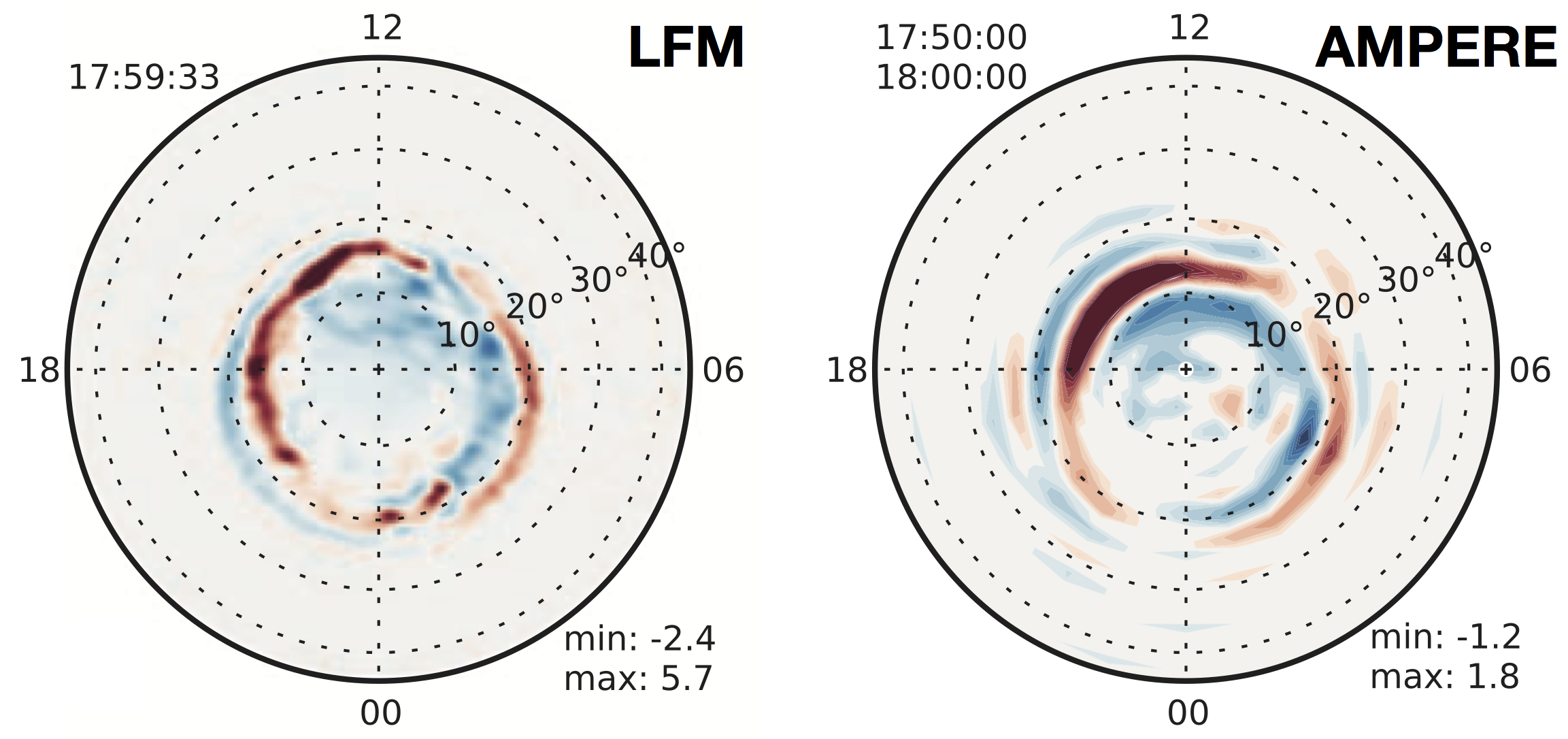
• For magnetospheric applications we have also completely rewritten the ionospheric solver from the LFM code (MIX) and integrated the new Fortran code with GAMERA. The new solver (dubbed reMIX) incorporates the standard LFM ionospheric conductivity model, including ionization by solar irradiance and magnetospheric electron precipitation.